2.1.4. Универсальный характер комбинированных логических элементов и-не и или-не. 2И не
Простейшие логические элементы Логический элемент 2и
Условное обозначение Логическая функция Таблица соответствия
| x1 | x2 | y |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
y=х1*х2
логический 0- низкий уровень напряжения;
логическая 1- высокий уровень напряжения.
Логический элемент 2или
Условное обозначение Логическая функция Таблица соответствия
| x1 | x2 | y |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
y = x1+x2
Логический элемент 3и
| x1 | x2 | x3 | y |
| 0 | | 0 | 0 |
| 0 | 1 | 0 | 0 |
| 1 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 1 |
y = x1*x2*x3
Логический элемент Исключающее или
Условное обозначение Логическая функция Таблица соответствия
| x1 | x2 | y |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
y =
Логическая функция Исключающее ИЛИ находит применение в схемах контроля на четность/нечетность. Так, контроль на четность n- разрядного двоичного кода{an-1..a0} выполняется путем аппаратной реализации следующего равенства:
an-1 Å an-2 Å ... Å a0 = 0
Комбинирование логических элементов
Комбинируя между собой рассмотренные простейшие логические элементы, можно реализовать и другие более сложные логические функции, например:
Инвертор Логическая схема 2И
Логическую функцию у = x1 * x2+ x3 можно преобразовать следующим образом:
В результате получим следующую реализацию этой функции на базовых логических элементах 2И-НЕ:
Аналогично, логическая функция на базовых элементах 2И-НЕ реализуется следующим образом:
Простейшие интегральные микросхемы средней степени интеграции
На рис. 2 представлены условные обозначения интегральных микросхем средней степени интеграции К555ЛА3 и К555ЛЕ1, содержащие в одном корпусе/на одном кристалле по 4 базовых элемента 2И-НЕ и 2ИЛИ-НЕ соответственно. Выводы микросхем 7, 14 используются для подачи на микросхему питания +5 В.
Выводы питания на принципиальных схемах обычно не обозначаются и подразумеваются по умолчанию. Питание подается одновременно на все 4 логических элемента микросхемы, хотя в конкретной схеме могут быть задействованы не все из них.
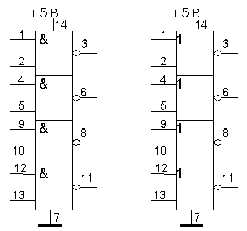
Рис. 2. Интегральные микросхемы
К555ЛА3 и К555ЛЕ1
На рис.3 приводятся условные обозначения ряда других простейших микросхем средней степени интеграции. Номера выводов микросхем не приводятся (их можно найти в справочниках по интегральным микросхемам):
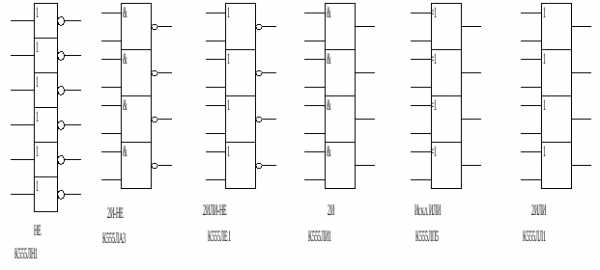
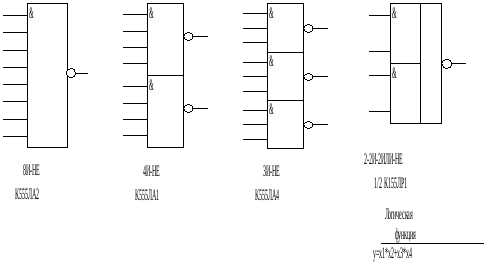
Рис. 3. Простейшие интегральные микросхемы
studfiles.net
2.1.4. Универсальный характер комбинированных логических элементов и-не и или-не
Логические элементы И-НЕиИЛИ-НЕнаиболее широко представлены в справочной литературе и обладают универсальными свойствами. На их основе можно построить все логические функции.
Реализация основных логических функций с помощью элемента И-НЕ. В табл. 2.3 представлены варианты реализации основных логических функций с помощью элементов И-НЕ, имеющих два входа.
Таблица 2.3
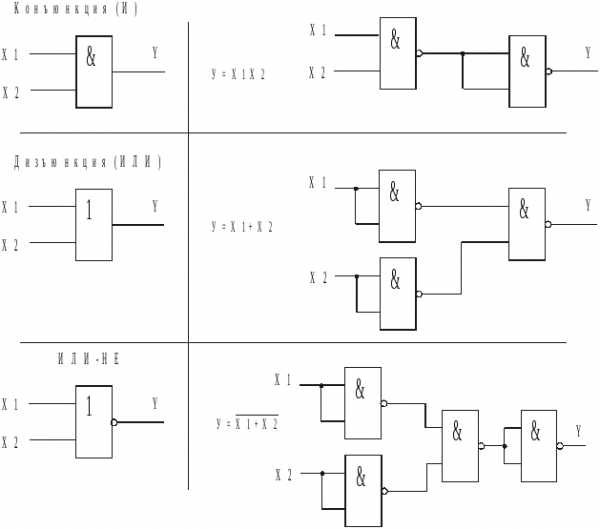
Реализация основных логических функций с помощью элемента ИЛИ-НЕ, имеющих два входа, показана в табл. 2.4.
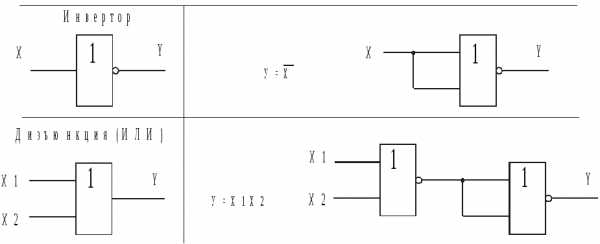 Таблица 2.4
Таблица 2.4
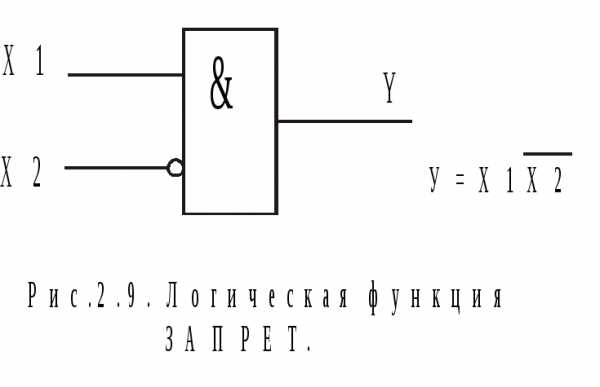
Если добавить к последней схеме инвертор, то получится элемент И-НЕ. Самостоятельное значение имеет логическая операцияЗАПРЕТ. Обозначение, аналитическое выражение и таблица истинности данной функции приводятся ниже.
| Х | Х1 | Y |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
Логический элемент ЗАПРЕТимеет в простейшем случае два входа: разрешающий или информационный (Х1) и запрещающий (Х2). Если на запрещающий вход поступает сигнал 1, то это соответствует запрету на передачу информации с информационного входа на выход.
О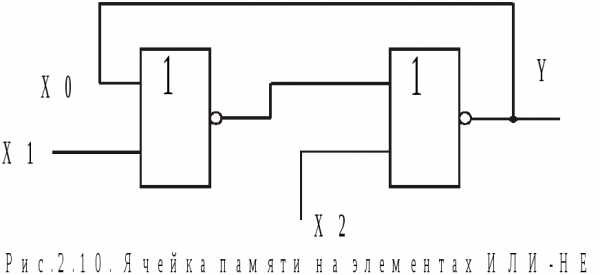 дним из важнейших элементов цифровых систем являетсяЯЧЕЙКА ПАМЯТИ. Она может быть построена на универсальных элементахИЛИ-НЕ(рис.2.10). Подача на вход Х1 единичного импульса при нулевом сигнале на входе Х2, дает на общем выходеY– единицу, которая по цепи обратной связи подается на вход Х0. При снятии сигнала со входа Х1, схема остается в том же состоянии, т.е. сохраняет записанную информацию. Для стирания этой информации служит вход Х2. Логическую операциюПАМЯТЬможно также реализовать с помощьюRS-триггера на элементахИ-НЕ.
дним из важнейших элементов цифровых систем являетсяЯЧЕЙКА ПАМЯТИ. Она может быть построена на универсальных элементахИЛИ-НЕ(рис.2.10). Подача на вход Х1 единичного импульса при нулевом сигнале на входе Х2, дает на общем выходеY– единицу, которая по цепи обратной связи подается на вход Х0. При снятии сигнала со входа Х1, схема остается в том же состоянии, т.е. сохраняет записанную информацию. Для стирания этой информации служит вход Х2. Логическую операциюПАМЯТЬможно также реализовать с помощьюRS-триггера на элементахИ-НЕ.
2.2. Анализ и синтез цифровых электронных схем
Основой для формального описания и оптимизации цифровых систем является математическая логика (алгебра Буля). Некоторые понятия математической логики были рассмотрены выше. Логические переменные и логические функции позволяют рассматривать дискретные схемы любой сложности, а также выполнять алгебраические преобразования с целью оптимизации схем. Данное направление в математической логике называется теорией конечных автоматов. Различают два типа конечных автоматов:
схемы, состояние выходных переменных которых зависит только от комбинации входных переменных – автоматы комбинационного типа;
схемы, состояние выходных переменных которых зависит не только от комбинации входных переменных, но и от состояния схемы в предыдущие моменты времени – автоматы последовательностного типа.
При рассмотрении логических структур не учитывают переходные процессы в электрических цепях автоматов. Считается, что переменные изменяются мгновенно в некоторые моменты времени и сохраняют свои значения на отрезках времени, которые называются тактами. Такты могут быть разной продолжительности. Начало тактов определяется синхронизирующими импульсами. Вместо параметра времени при описании систем используют номер такта. В последовательностных схемах существенную роль играют внутренние состояния автомата, которые задаются вектором промежуточных переменных. Этот вектор и значения входных переменных позволяют определить выходные переменные в данный тактовый момент и состояние в следующий такт. Описание работы автоматов иллюстрируется таблицами и графами. Они широко применяются для анализа, синтеза и оптимизации дискретных схем.
studfiles.net
2.3.2. Универсальный характер логического элемента и-не.
С помощью достаточного количества логических элементов И-НЕ можно реализовать любую логическую функцию.
| Логическая функция | Условное обозначение | Схема с использованием только логического элемента И-НЕ |
| Инвертор | ||
| И | ||
| ИЛИ | ||
| ИЛИ-НЕ | ||
| Исключающее ИЛИ | | |
| Исключающее ИЛИ-НЕ |
2.3.3. Логические элементы с числом входов больше двух
Помимо двухвходовых логических элементов широко применяются логические элементы с числом входов больше 2. Рассмотрим трехвходовый элемент И (3И). На рисунке 2.6 справа.
Рисунок 2.6 - Трехвходовый элемент И (справа)и его схема на двухвходовых элементах И (слева).
Нетрудно получить булево выражение для трехвходового элемента У=Х1·Х2·Х3
Таблица истинности:
| X1 | X2 | X3 | Y |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 |
Трехвходовый элемент И реализован внутри микросхем К155ЛИ3, К155ЛИ4
2.3.4. Интегральные схемы
Все логические элементы физически располагаются внутри интегральных схем (микросхем). Рассмотрим, например, микросхемы реализующие логическую функцию И серии 155: К155ЛИ1, К155ЛИ2, К155ЛИ3, К155ЛИ4, К155ЛИ5, К155ЛИ6.
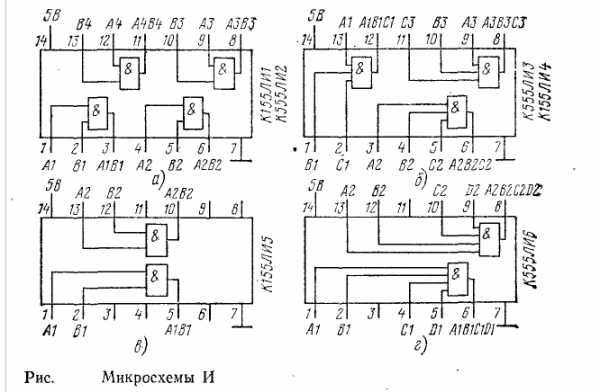
Рисунок 2.7 - Размещение логических элементов внутри корпусов микросхем.
Как видим, к 14 ножке микросхем прикладывается питающее напряжение +5В, к 7 ножке микросхем – напряжение 0В, остальные ножки задействованы для выводов элементов И. На электрических принципиальных схемах ножки питания могут не показывать, но это не значит, что питание не требуется подводить, как и любые другие электронные устройства микросхемы требуют питания.
2.3.5. Конструирование схемы по таблице истинности.
Рассмотрим задачу: пусть требуется открыть кодовый электрический замок кодом 111 или кодом 010. При этом будем считать, что если на выходе схемы 0, то замок закрыт, а если 1, то открыт. Составим таблицу истинности.
| X1 | X2 | X3 | Y (состояние замка) |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 |
В основе схемы лежит элемент ИЛИ два входа, которого соответствуют двум кодам открывающим замок. Проверка кодов осуществляется трехвходовыми элементами И.
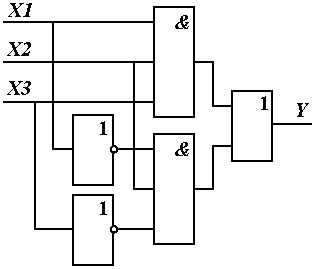
Рисунок 2.8 - Схема кодового замка
2.4. Классификация цифровых схем
Схемы с логическими элементами могут принадлежать к одному из 2 видов: комбинированные и последовательные.
К комбинированным относятся такие, у которых значение выхода не зависит от значений входа в предыдущий момент времени, т.е. значение сигнала на выходе полностью определяется текущим состоянием входов. К ним относят: мультиплексоры и демультиплексоры, шифраторы и дешифраторы, сумматоры и вычитатели, преобразователи входов и т.д.
К последовательным схемам относят такие, у которых значение на выходе зависит не только от текущего состояния входа и выхода, но и от состояния входов и выходов в предыдущий момент времени. К ним относят все схемы на триггерах, счетчики.
studfiles.net
Цифровые микросхемы Виды цифровых микросхем.
В настоящее время используется несколько видов логических элементов:
диодно-транзисторная логика (ДТЛ)
транзисторно-транзисторная логика (ТТЛ, TTL)
логика на основе комплементарных МОП транзисторов (КМОП, CMOS)
логика на основе сочетания комплементарных МОП и биполярных транзисторов (BiCMOS)
Первоначально получили распространение цифровые микросхемы, построенные на основе ТТЛ технологии. Поэтому до сих пор существует огромное количество микросхем, построенных по этой технологии или совместимые с этими микросхемами по напряжению питания, логическим уровням и цоколёвке.
Диодно-транзисторная логика (дтл)
Наиболее простой логический элемент получается при помощи диодов. Схема такого элемента приведена на рис. 1.
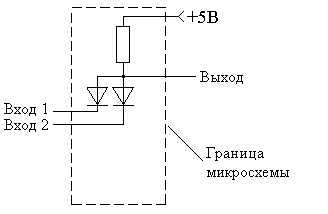
Рис. 1. Принципиальная схема логического элемента "2И", выполненного на диодах.
В этой схеме при подаче нулевого потенциала на любой из входов (или на оба сразу) через резистор будет протекать ток и на его сопротивлении возникнет падение напряжения. В результате на выходе схемы единичный потенциал будет только если подать единичный потенциал сразу на оба входа микросхемы. То есть схема реализует функцию "2И".
Количество входов элемента "И" зависит от количества диодов. Если использовать два диода, то получится элемент "2И", если три диода - то "3И", если четыре диода, то "4И", и так далее. В микросхемах выпускается максимальный элемент "8И".
Недостатком ДТЛ является низкая нагрузочная способность. Поэтому к схеме диодного логического элемента "И" обычно подключается двухтактный усилитель на биполярных транзисторах
Транзисторно-транзисторная логика (ттл)
Технологически логику удобней реализовать на транзисторе с несколькими дополнительными эмиттерами. В ТТЛ схемах вместо параллельного соединения диодов используется многоэмиттерный транзистор. Принцип работы этого элемента не отличается от работы диодного элемента "2И". Высокий потенциал на выходе многоэмиттерного транзистора получается только в том случае, когда на обоих входах элемента (эмиттерах транзистора) присутствует высокий потенциал и все эмиттерные переходы заперты (т.е. нет эмиттерного тока). Принципиальная схема типового элемента ТТЛ микросхемы приведена на рис. 2.
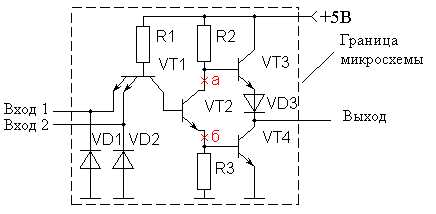
Рис. 2. Принципиальная схема типового элемента ТТЛ микросхемы.
Усилитель инвертирует сигнал на выходе схемы. По такой схеме выполнены базовые элементы микросхем серий 130, 131, 133, 134, 155. Элемент "И-НЕ" в этих сериях микросхем обычно имеет обозначение ЛА. Например, схема К155ЛА3 содержит в одном корпусе четыре элемента "2И-НЕ". На основе базового элемента строится и инвертор. В этом случае на входе используется только один диод
При необходимости объединения нескольких логических элементов "И" по схеме "ИЛИ" (или при реализации логических элементов "ИЛИ") транзисторы VT2 соединяются параллельно в точках "а" и "б", показанных на рис.2, а выходной каскад используется один. Принципиальная схема логического элемента "2И-2ИЛИ-НЕ" приведена на рис.3.
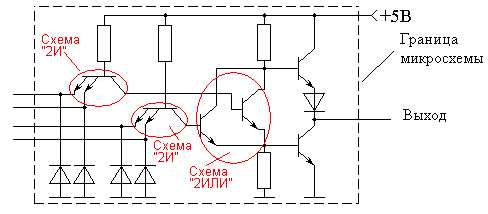
Рис. 3. Принципиальная схема ТТЛ микросхемы "2И-2ИЛИ-НЕ".
Такие элементы содержатся в цифровых микросхемах с обозначением ЛР.
Схемы "ИЛИ-НЕ" в ТТЛ сериях микросхем обычно имеет обозначение ЛЕ. Например схема К1531ЛЕ5 содержит в одном корпусе четыре элемента "2ИЛИ-НЕ".
studfiles.net
Реализация основных логических операций И, ИЛИ, НЕ на базе логических элементов И-НЕ, ИЛИ-НЕ.
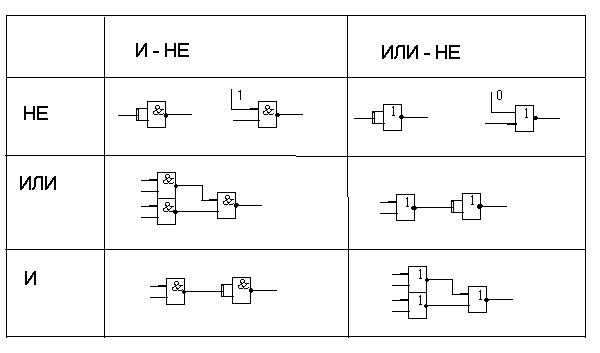
Элементы «2И–НЕ» и «2ИЛИ–НЕ» называются базовыми логическими элементами. Используя перечисленные элементы можно создать любое устройство.
Правило записи переключательной функции по таблице истинности
Рассмотрим для примера таблицу истинности элемента «ИЛИ».
| X1 | X2 | Y |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Общее правило формулируется так:
1 Выделяют строки, в которых Y принимает единичное значение.
2 Для каждой из выделенных строк составляют минтерм – частное произведение всех входных переменных или их отрицаний. Причем Xi входит в минтерм без знака инверсии, если в выделенной строке Xi=1 и со знаком инверсии в противном случае.
3 Составляют логическую сумму всех полученных минтермов и получают совершенную дизъюнктивно нормальную форму записи переключательной функции.
4 Осуществляют минимизацию одним из известных методов и получают минимизированную дизъюнктивно-нормальную форму записи переключательной функции. Схемотехнической реализации подлежит только МНДФ.
Замечание: если число строк, в которых функция принимает нулевое значение больше, чем число, в которых функция принимает единичное значение, то можно найти инверсное значение переключательной функции, пользуясь тем же правилом.
Минимизация полученных переключательных функций проводится при помощи карт Вейча или диаграмм Карно.
Комбинационные логические схемы.
Комбинационные логические схемы – схемы, выходной сигнал которых в рассматриваемый момент времени зависит от комбинации входных сигналов в этот момент времени.
8. Логический элемент ИСКЛЮЧАЮЩЕЕ ИЛИ: схемная реализация на базовых логических элементах.
x1
x1
y y
x2 x2
x1
x2
y
Похожие статьи:
poznayka.org
Логические элементы - это... Что такое Логические элементы?
Логические элементы — устройства, предназначенные для обработки информации в цифровой форме (последовательности сигналов высокого — «1» и низкого — «0» уровней в двоичной логике, последовательность «0», «1» и «2» в троичной логике, последовательности «0», «1», «2», «3», «4», «5», «6», «7», «8» и «9» в десятичной логике). Физически логические элементы могут быть выполнены механическими, электромеханическими (на электромагнитных реле), электронными (на диодах и транзисторах), пневматическими, гидравлическими, оптическими и др.
С развитием электротехники от механических логических элементов перешли к электромеханическим логическим элементам (на электромагнитных реле), а затем к электронным логическим элементам на электронных лампах, позже — на транзисторах. После доказательства в 1946 г. теоремы Джона фон Неймана об экономичности показательных позиционных систем счисления стало известно о преимуществах двоичной и троичной систем счисления по сравнению с десятичной системой счисления. От десятичных логических элементов перешли к двоичным логическим элементам. Двоичность и троичность позволяет значительно сократить количество операций и элементов, выполняющих эту обработку, по сравнению с десятичными логическими элементами.
Логические элементы выполняют логическую функцию (операцию) над входными сигналами (операндами, данными).
Всего возможно логических функций и соответствующих им логических элементов, где — основание системы счисления, — число входов (аргументов), — число выходов, то есть бесконечное число логических элементов. Поэтому в данной статье рассматриваются только простейшие и важнейшие логические элементы.
Всего возможны двоичных двухвходовых логических элементов и двоичных трёхвходовых логических элементов (Булева функция).
Кроме 16 двоичных двухвходовых логических элементов и 256 трёхвходовых двоичных логических элементов возможны 19 683 двухвходовых троичных логических элемента и 7 625 597 484 987 трёхвходовых троичных логических элементов (троичные функции).
|
Содержание
|
Логические операции (булева функция) своё теоретическое обоснование получили в алгебре логики.
Логические операции с одним операндом называются унарными, с двумя — бинарными, с тремя — тернарными (триарными, тринарными) и т. д.
Из возможных унарных операций с унарным выходом интерес для реализации представляют операции отрицания и повторения, причём, операция отрицания имеет большую значимость, чем операция повторения, так как повторитель может быть собран из двух инверторов, а инвертор из повторителей не собрать.
Отрицание, НЕ
Инвертор, НЕ| 0 | 1 |
| 1 | 0 |
Мнемоническое правило для отрицания звучит так: На выходе будет:
Повторение, ДА
| 0 | 0 |
| 1 | 1 |
Преобразование информации требует выполнения операций с группами знаков, простейшей из которых является группа из двух знаков. Оперирование с большими группами всегда можно разбить на последовательные операции с двумя знаками.
Из возможных бинарных логических операций с двумя знаками c унарным выходом интерес для реализации представляют 10 операций, приведённых ниже.
Конъюнкция (логическое умножение). Операция 2И. Функция min(A,B)
2И| 0 | 0 | 0 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 1 | 1 |
Логический элемент, реализующий функцию конъюнкции, называется схемой совпадения. Мнемоническое правило для конъюнкции с любым количеством входов звучит так: На выходе будет:
- «1» тогда и только тогда, когда на всех входах действуют «1»,
- «0» тогда и только тогда, когда хотя бы на одном входе действует «0»
Дизъюнкция (логическое сложение). Операция 2ИЛИ. Функция max(A,B)
2ИЛИМнемоническое правило для дизъюнкции с любым количеством входов звучит так: На выходе будет:
- «1» тогда и только тогда, когда хотя бы на одном входе действует «1»,
- «0» тогда и только тогда, когда на всех входах действуют «0»
Инверсия функции конъюнкции. Операция 2И-НЕ (штрих Шеффера)
2И-НЕМнемоническое правило для И-НЕ с любым количеством входов звучит так: На выходе будет:
- «1» тогда и только тогда, когда хотя бы на одном входе действует «0»,
- «0» тогда и только тогда, когда на всех входах действуют «1»
Инверсия функции дизъюнкции. Операция 2ИЛИ-НЕ (стрелка Пирса)
2ИЛИ-НЕ| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
Мнемоническое правило для ИЛИ-НЕ с любым количеством входов звучит так: На выходе будет:
- «1» тогда и только тогда, когда на всех входах действуют «0»,
- «0» тогда и только тогда, когда хотя бы на одном входе действует «1»
Эквивалентность (равнозначность), 2ИСКЛЮЧАЮЩЕЕ_ИЛИ-НЕ
ИСКЛ-ИЛИ-НЕ| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Мнемоническое правило эквивалентности с любым количеством входов звучит так: На выходе будет:
- «1» тогда и только тогда, когда на входе действует четное количество,
- «0» тогда и только тогда, когда на входе действует нечетное количество
Сложение по модулю 2 (2Исключающее_ИЛИ, неравнозначность). Инверсия равнозначности.
ИСКЛ-ИЛИВ англоязычной литературе 2XOR.
Мнемоническое правило для суммы по модулю 2 с любым количеством входов звучит так: На выходе будет:
- «1» тогда и только тогда, когда на входе действует нечётное количество ,
- «0» тогда и только тогда, когда на входе действует чётное количество
Импликация от A к B (прямая импликация, инверсия декремента, A<=B)
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Мнемоническое правило для инверсии декремента звучит так: На выходе будет:
- «0» тогда и только тогда, когда на «B» меньше «А»,
- «1» тогда и только тогда, когда на «B» больше либо равно «А»
Импликация от B к A (обратная импликация, инверсия инкремента, A>=B)
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Мнемоническое правило для инверсии инкремента звучит так: На выходе будет:
- «0» тогда и только тогда, когда на «B» больше «А»,
- «1» тогда и только тогда, когда на «B» меньше либо равно «А»
Декремент. Запрет импликации по B. Инверсия импликации от A к B
Мнемоническое правило для инверсии импликации от A к B звучит так: На выходе будет:
- «1» тогда и только тогда, когда на «A» больше «B»,
- «0» тогда и только тогда, когда на «A» меньше либо равно «B»
Инкремент. Запрет импликации по A. Инверсия импликации от B к A
Мнемоническое правило для инверсии импликации от B к A звучит так: На выходе будет:
- «1» тогда и только тогда, когда на «B» больше «A»,
- «0» тогда и только тогда, когда на «B» меньше либо равно «A»
Примечание 1. Элементы импликаций не имеют промышленных аналогов для функций с количеством входов, не равным 2.Примечание 2. Элементы импликаций не имеют промышленных аналогов.
Этими простейшими логическими операциями (функциями), и даже некоторыми их подмножествами, можно выразить любые другие логические операции. Такой набор простейших функций называется функционально полным логическим базисом. Таких базисов 4:
- И, НЕ (2 элемента)
- ИЛИ, НЕ (2 элемента)
- И-НЕ (1 элемент)
- ИЛИ-НЕ (1 элемент).
Для преобразования логических функций в один из названых базисов необходимо применять Закон (правило) де-Моргана.
Физические реализации логических элементов
Физические реализации одной и той же логической функции в разных системах электронных и неэлектронных элементов отличаются друг от друга.
Классификация электронных транзисторных физических реализаций логических элементов
Логические элементы подразделяются и по типу использованных в них электронных элементов. Наибольшее применение в настоящее время находят следующие логические элементы:
- РТЛ (резисторно-транзисторная логика)
- ДТЛ (диодно-транзисторная логика)
- ТТЛ (транзисторно-транзисторная логика)
Обычно входной каскад логических элементов ТТЛ представляет собой простейшие компараторы, которые могут быть выполнены различными способами (на многоэмиттерном транзисторе или на диодной сборке). В логических элементах ТТЛ входной каскад, кроме функций компараторов, выполняет и логические функции. Далее следует выходной усилитель с двухтактным (двухключевым) выходом.
В логических элементах КМОП входные каскады также представляют собой простейшие компараторы. Усилителями являются КМОП-транзисторы. Логические функции выполняются комбинациями параллельно и последовательно включенных ключей, которые одновременно являются и выходными ключами.
Транзисторы могут работать в инверсном режиме, но с меньшим коэффициентом усиления. Это свойство используются в ТТЛ многоэмиттерных транзисторах. При подаче на оба входа сигнала высокого уровня (1,1) первый транзистор оказывается включенным в инверсном режиме по схеме эмиттерного повторителя с высоким уровнем на базе, транзистор открывается и подключает базу второго транзистора к высокому уровню, ток идёт через первый транзистор в базу второго транзистора и открывает его. Второй транзистор «открыт», его сопротивление мало и на его коллекторе напряжение соответствует низкому уровню (0). Если хотя бы на одном из входов сигнал низкого уровня (0), то транзистор оказывается включенным по схеме с общим эмиттером, через базу первого транзистора на этот вход идёт ток, что открывает его и он закорачивает базу второго транзистора на землю, напряжение на базе второго транзистора мало и он «закрыт», выходное напряжение соответствует высокому уровню. Таким образом, таблица истинности соответствует функции 2И-НЕ.
Для увеличения быстродействия логических элементов в них используются транзисторы Шоттки (транзисторы с диодами Шоттки), отличительной особенностью которых является применение в их конструкции выпрямляющего контакта металл-полупроводник вместо p-n перехода. При работе этих приборов отсутствует инжекция неосновных носителей и явления накопления и рассасывания заряда, что обеспечивает высокое быстродействие. Включение этих диодов параллельно коллекторному переходу блокирует насыщение выходных транзисторов, что увеличивает напряжения логических 0 и 1, но уменьшает потери времени на переключение логического элемента при том же потребляемом токе (или позволяет уменьшить потребляемый ток при сохранении стандартного быстродействия). Так, серия 74хх и серия 74LSxx имеют приблизительно равное быстродействие (в действительности, серия 74LSxx несколько быстрее), но потребляемый от источника питания ток меньше в 4-5 раз (во столько же раз меньше и входной ток логического элемента).
Эта логика, иначе называемая логикой на переключателях тока, построена на базе биполярных транзисторов, объединённых в дифференциальные каскады. Один из входов обычно подключён внутри микросхемы к источнику опорного (образцового) напряжения, примерно посредине между логическими уровнями. Сумма токов через транзисторы дифференциального каскада постоянна, в зависимости от логического уровня на входе изменяется лишь то, через какой из транзисторов течёт этот ток. В отличие от ТТЛ, транзисторы в ЭСЛ работают в активном режиме и не входят в насыщение или инверсный режим. Это приводит к тому, что быстродействие ЭСЛ-элемента при той же технологии (тех же характеристиках транзисторов) гораздо больше, чем ТТЛ-элемента, но больше и потребляемый ток. К тому же, разница между логическими уровнями у ЭСЛ-элемента намного меньше, чем у ТТЛ (меньше вольта), и, для приемлемой помехоустойчивости, приходится использовать отрицательное напряжение питания (а иногда и применять для выходных каскадов второе питание). Зато максимальные частоты переключения триггеров на ЭСЛ более, чем на порядок превышают возможности современных им ТТЛ, например, серия К500 обеспечивала частоты переключения 160—200 МГц, по сравнению с 10-15 МГц современной ей ТТЛ серии К155. В настоящее время и ТТЛ(Ш), и ЭСЛ практически не используются, так как с уменьшением проектных норм КМОП технология достигла частот переключения в несколько гигагерц.
Инвертор
Одним из основных логических элементов является инвертор. Инвертирующими каскадами являются однотранзисторный каскад с общим эмиттером, однотранзисторный каскад с общим истоком, двухтранзисторный двухтактный выходной каскад на комплементарных парах транзисторов с последовательным включением транзисторов по постоянному току (применяется в ТТЛ и КМОП), двухтранзисторный дифференциальный каскад с параллельным включением транзисторов по постоянному току (применяется в ЭСЛ) и др. Но одного условия инвертирования недостаточно для применения инвертирующего каскада в качестве логического инвертора. Логический инвертор должен иметь смещённую рабочую точку на один из краёв проходной характеристики, что делает каскад неустойчивым в середине диапазона входных величин и устойчивым в крайних положениях (закрыт, открыт). Такой характеристикой обладает компаратор, поэтому логические инверторы строят как компараторы, а не как гармонические усилительные каскады с устойчивой рабочей точкой в середине диапазона входных величин. Таких каскадов, как и контактных групп реле, может быть два вида: нормально закрытые (разомкнутые) и нормально открытые (замкнутые).
Применение логических элементов
Логические элементы входят в состав микросхем, например ТТЛ элементы — в состав микросхем К155 (SN74), К133; ТТЛШ — 530, 533, К555, ЭСЛ — 100, К500 и т. д.
Комбинационные логические устройства
Комбинационными называются такие логические устройства, выходные сигналы которых однозначно определяются входными сигналами:
Все они выполняют простейшие двоичные, троичные или n-ичные логические функции.
Последовательностные цифровые устройства
Последовательностными называют такие логические устройства, выходные сигналы которых определяются не только сигналами на входах, но и предысторией их работы, то есть состоянием элементов памяти.
См. также
Ссылки
Литература
dic.academic.ru

 2
2